课程代码[ 570024 ] 课程类别[专业基础课]
学 分 [ 4.0 ] 学 时 [ 64 ]
开课部门[思政基础部]
适用专业[ 船工系、机电系]
制 定 人[ 数学教研室] 制定日期[2020年5月]
审 核 人[系部负责人] 审核日期[2020年6月]
一、课程性质与任务
高等数学是我院文理科非数学专业学生学习的一门必修的重要基础理论课程,是为培养我国社会主义现代化建设所需要的高质量专门人才服务的。一方面,它为学生学习专业课程和解决实际问题提供必不可少的数学基础知识及常用的数学方法;另一方面,教师要通过各个教学环节,使用各种教学手段逐步培养学生使其具有数学运算能力、抽象思维能力、空间想象能力、科学创新能力,尤其具有综合运用数学知识、数学方法结合所学专业知识去分析和解决实际问题的能力。
二、课程目标
(一)总体目标
众所周知,随着科学技术的发展,计算机的广泛应用,数学已经渗透到社会生活的各个领域,《高等数学》在高等院校理工科、经济类、管理类各专业中是一门重要的公共基础理论课,是学生的必修课。
通过本课程的学习,力求使学生较系统地获得微积分、线性代数和概率统计的基础知识、必要的基础理论和常用的运算方法。
通过本课程的学习,使学生受到基本数学方法、思维的训练。
通过本课程的学习,使学生得到运用这些方法解决简单的实际问题的初步训练。
通过本课程的学习,为学生学习相关专业的后继课程和进一步扩大数学知识以及解决实际问题提供必要的数学基础。
通过本课程的学习培养学生良好的综合素质:具有思维敏捷、灵活应变的能力;具有严谨、稳重、扎实的行为习惯;具有宽容大度、耐心、细致的心理品质;具有不断探索、锐意进取的思想意识以及团结协作的团队精神。
1.知识目标
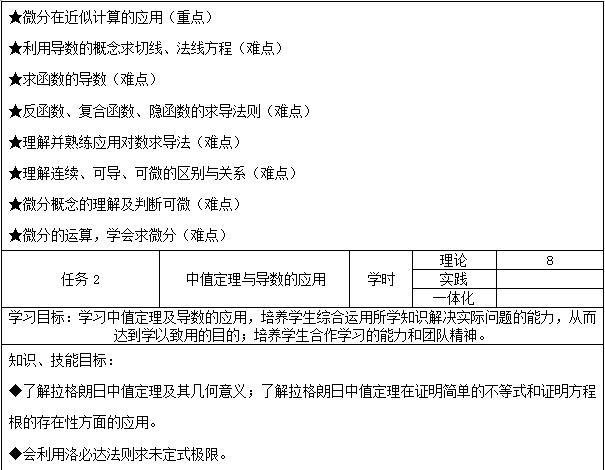
理解函数的有关概念及性质;掌握基本初等函数及其图形的有关知识;理解函数连续的概念,了解连续函数的性质。
理解极限概念,掌握求极限的几种基本方法。
理解导数、微分的概念,掌握求导方法并能利用导数、微分的知识解决有关的简单的实际问题。
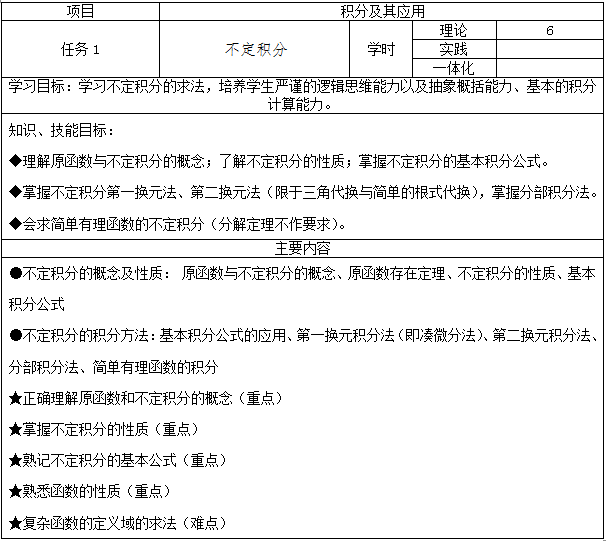
理解原函数与不定积分的概念;掌握不定积分的基本积分公式及常见的积分方法。
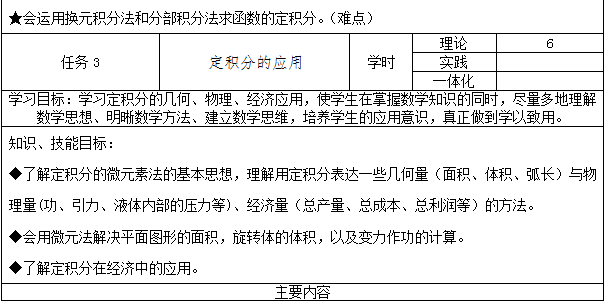
理解定积分的概念,掌握牛顿—莱布尼兹公式和定积分的积分法;能用定积分解决简单的实际问题。
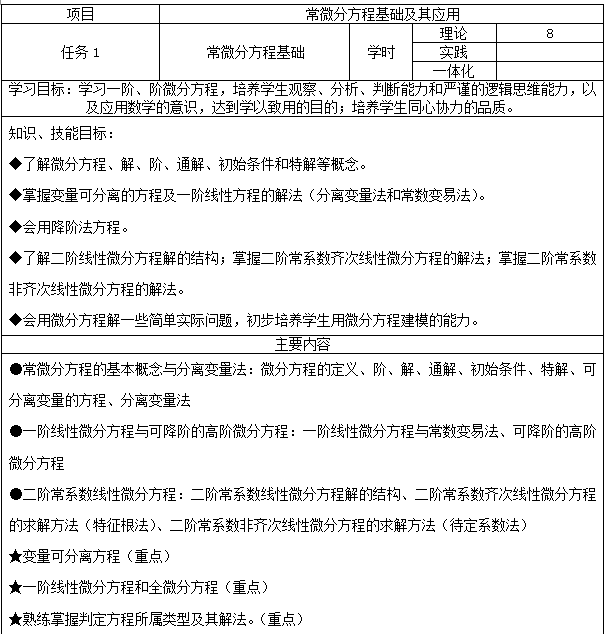
了解微分方程的有关概念,掌握较简单的微分方程的解法,了解简单的建模方法。
2.技能目标
进行准确、灵活、快速的极限、导数、积分的基本计算。
运用所学知识分析和解决实际问题:运用导数解决生活中的极值与最值问题;运用微分求近似值;运用定积分解决不规则图形的面积的计算、几何体体积的计算、变力做功的计算以及一些常见的经济问题的计算。
3.素质目标
提升自我控制能力,认同组织的使命与愿景,在遭受诱惑、阻力、敌意、压力、受激时,保持冷静、抑制负面情绪或行动,自我控制能力强。
培养质量意识、工程规范意识、严谨的学风,充分执行、重复应用、准确遵守(言行一致),在执行过程中,认真听候命令、无选择性的执行、不违犯制度和流程;爱岗敬业,工作勤奋踏实,为企(事)业坚持不懈地努力工作,认真负责,一丝不苟。
培养实用技能,通过对理论知识的学习,要求学生能将所学应用到具体的生活中解决实际的问题,做到“学中做,做中学”,学以致用。
培养团队精神——组织沟通,利用分组讨论、练习,培养学生与人团结协作、相互沟通能力,使其具有合作精神、协调工作和组织管理能力。
培养良好的心理素质——不怕挫折,勇于进取。
三、课程设计
(一)课程设计思路
本课程设计以培养学生的数学应用能力和数学素质为教育目标,遵循“以应用为目的,以必需够用为度”的原则,建立符合专业需求的内容体系、突出数学应用能力培养、将数学建模的思想与方法引入高职数学课堂,创新高职教育特色的课程教学模式。推行“问题解决”的教学模式,将教学过程概括为“提出实践问题——教授相关的数学知识——建立数学模型——解决实践问题”。充分发挥高等数学课程在人才培养中的重要作用。
(二)课程内容与教学要求
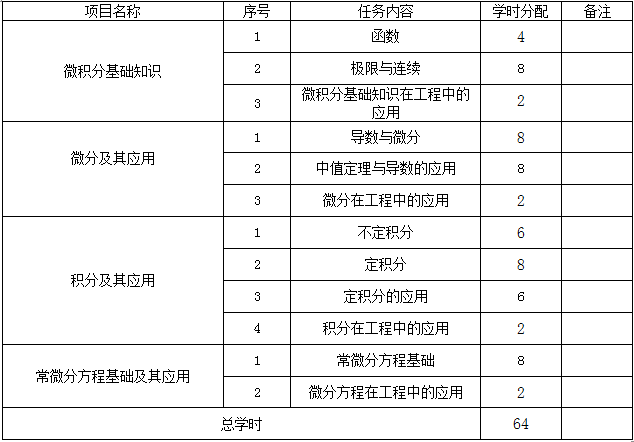
1.课时分配表
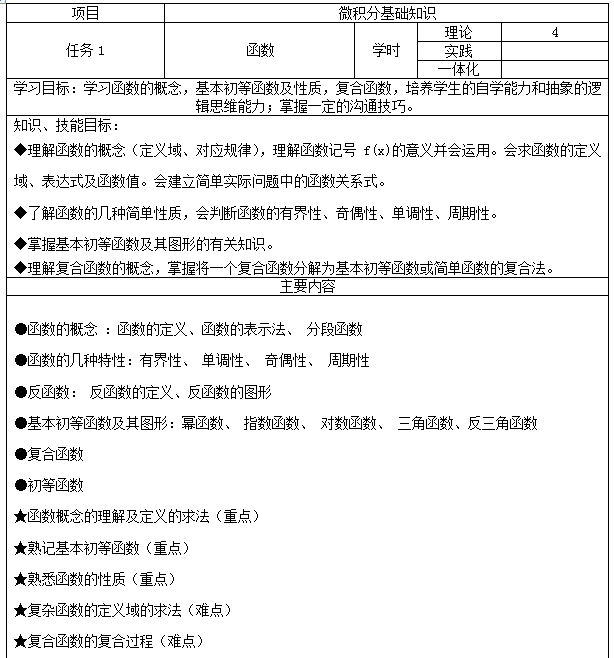
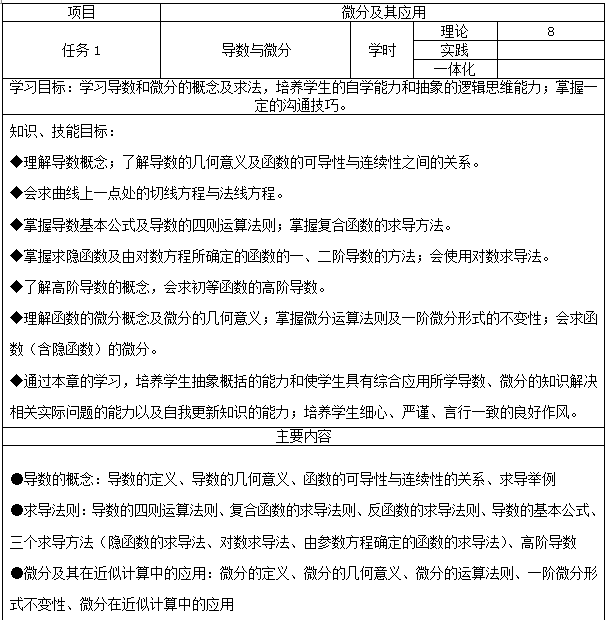
2.任务设计

















四、课程实施
(一)教学方法建议
本课程的教学自始至终贯穿快乐学习的教学理念,以学生为本,突出学生的主体地位。要用到的主要方法有:讲授、培训、破冰法、头脑风暴、案例分析、小组讨论、专家辅导、教练技术、课堂(后)练习等。
1、讲授与培训
高等数学各章节中的概念、定理、公式、方法等知识点一般采用讲授与培训的教学方法。教师在教学过程中,不仅仅是传授知识,让学生知道和理解知识,更重要的是要求通过培训技术手段,将知识转化为学生的技能和能力。同时使学生的行为(心度、态度等)发生改变或转变。
2、头脑风暴、小组讨论与练习
本课程致力于培养和提升学生的计算能力、思维能力、观察能力及合作精神,在概念、定理、公式的应用等方面,可以采用教师讲授、示范、小组讨论与练习相结合的方法进行,从而找到解决问题的最佳途径和适合学生学习的最佳方法。
3、案例分析
对于与实际密切结合的知识点,可以专门安排相应的案例,引导、加深学生对知识的理解和把握,突出数学的实用性。
相关知识点:
微分在近似计算中的应用
函数的极值与最值
定积分的应用
线性规划问题
概率统计应用。
4、专家辅导与教练技术
针对不同层次的学生,采用不同的教学方法与学习方法,重点指导优等生和学困生的学习,指导学生解决学习中遇到的困难。
要求教师通过完善学生的心智模式来发挥其潜能,提升学习或工作效率:教师以中立的身份,通过运用聆听、发问等教练技巧反映出学生的心态,从而辩识其行为的正确性,并给予直接的反馈,使学生了解和洞悉自己、及时调整心态、清晰目标、激发潜能。
5、破冰法
在本课程开始前组织富有活力的游戏帮助学生建立起愉悦、积极的团队氛围;或根据某堂课的教学内容在课前创设适当的教学情境破冰,为学生参与后阶段的学习做准备。
6、课堂(后)练习
每次新授内容均可安排一次课堂(或课后)练习,以加深学生对知识的理解和掌握;题量以2-3题为宜,体现层次性。
(二)师资条件要求
1、数学专业本科或以上学历,能清楚地了解本专业的知识结构和能力要求。
2、两年以上的职业工作教学经验。
3、对高等数学有较深入的研究,熟悉数学在其他专业课程中的应用,能结合社会经济运用教学。
4、有良好的教师职业素养和科学先进的教学方法,具有一定的研修能力和教学计划执行力。
5、深刻理解企业人才素质培养方法,了解快乐学习的教学技巧。
(三)教学条件基本要求
1、硬件
多媒体教室、数学实验室。
2、软件
教学环境(舒适、安静)。
教师对学生的服务(包括教师出勤、下班辅导)。
(四)教学资源基本要求
1、选用教材:《微积分基础与应用》秦道炬 李兰兰主编,电子科技大学出版社出版。
2、参考教材:高等教育出版社、中国财政经济出版社以及湖南教育出版社的教材。
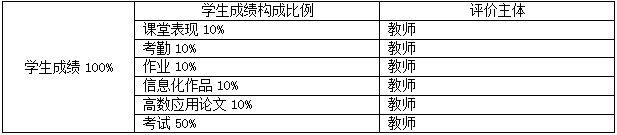
五、教学评价、考核要求
评价建议应体现多元评价方法,重视教学过程评价,突出阶段评价、目标评价、理论与实践一体化评价等,注重学生动手能力和在实践中分析问题、解决问题能力的考核,关注学生个别差异,鼓励学生创新实践。如: